Bayes Consistency vs. H-Consistency
[Summary & Contributions] | [Relevant Publications]
Summary and Contributions
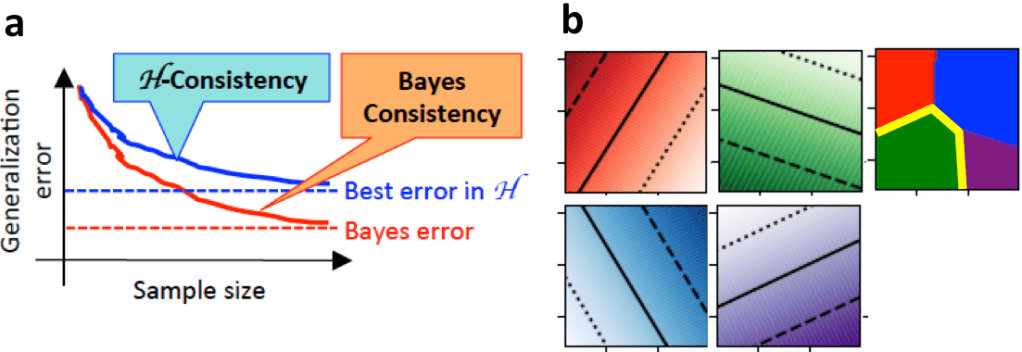
A popular class of algorithms in machine learning — namely, the broad class of surrogate risk minimization algorithms — is based on minimizing a continuous, convex surrogate loss instead of the discrete (and hard-to-minimize) target loss of interest. It is then important to ask what sorts of convergence properties such algorithms satisfy. There are two fundamental notions of convergence or ‘consistency’ that are widely studied for machine learning algorithms: Bayes consistency, which has its origins in statistical decision theory and requires convergence to a Bayes optimal model, and H-consistency, which has its origins in theoretical computer science and requires convergence only to the best model in some pre-specified class of models H. While minimizing a calibrated surrogate loss over a suitably large class of scoring models ensures Bayes consistency, it has been observed that minimizing a calibrated surrogate loss over a restricted class of scoring models related to H can fail to achieve H-consistency. In our work, we shed light on this apparent conundrum by highlighting the role of the class of scoring models over which the surrogate loss is minimized, and by demonstrating that by choosing this class carefully, one can potentially restore H-consistency of surrogate risk minimization methods. In particular, a key contribution of our work was the observation that the one-vs-all decision boundaries of multiclass linear models are not linear, and therefore minimizing one-vs-all surrogates over linear scoring models cannot be expected to provide H-consistency for linear models H (see figure below); based on this observation, we provided an alternative class of scoring models and corresponding algorithm that does achieve H-consistency in this setting.
Relevant Publications
- Mingyuan Zhang and Shivani Agarwal.
Bayes consistency vs. H-consistency: The interplay between surrogate loss functions and the scoring function class.
In Advances in Neural Information Processing Systems (NeurIPS), 2020.
Spotlight paper.
[pdf]