Hierarchical Classification
[Summary & Contributions] | [Relevant Publications]
Summary and Contributions
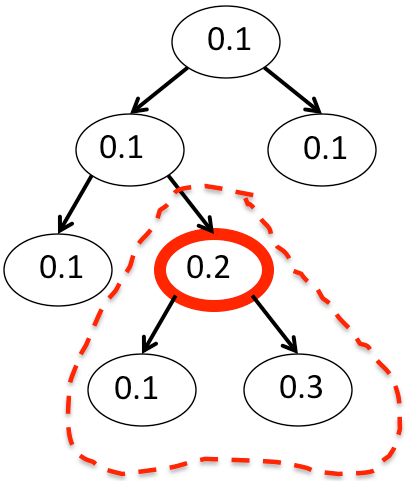
In many applications of machine learning that involve a large number of classes – including various document classification tasks, biological classification tasks, emotion recognition tasks, and others – the classes are naturally organized in a tree-like hierarchy. In such settings, the tree-distance loss is often used to evaluate learned prediction models. We developed fundamental theoretical understanding for this problem and designed the first known statistically consistent learning algorithms for such tasks – in particular, we showed that the Bayes optimal predictor for the tree-distance loss classifies instances according to the deepest node in the tree hierarchy whose conditional label probability is at least 1/2 (see figure below), and used this insight to design statistically consistent learning algorithms for hierarchical classification. Our algorithms make use of our results on multiclass learning with a reject option as a subroutine, and outperform previous state-of-the-art algorithms both in terms of generalization performance and in terms of scaling to large data sets.
Relevant Publications
- Harish G. Ramaswamy, Ambuj Tewari, and Shivani Agarwal.
Consistent algorithms for multiclass classification with an abstain option.
Electronic Journal of Statistics, 12(1):530-554, 2018.
[pdf] - Harish G. Ramaswamy, Ambuj Tewari and Shivani Agarwal.
Convex calibrated surrogates for hierarchical classification.
In Proceedings of the 32nd International Conference on Machine Learning (ICML), 2015.
[pdf]