Surrogate Loss Functions in Machine Learning (and Convex Calibration Dimension)
[Summary & Contributions] | [Relevant Publications]
Summary and Contributions
In many machine learning problems, we effectively try to solve some optimization problem — we try to find a model that somehow best fits the data. In recent years, there has been much work on designing better optimization algorithms. An orthogonal but equally important question is: Which optimization problem should we solve in the first place? This is because in many machine learning problems, the true loss or true objective that we care about is discrete and often computationally hard to minimize directly, and so we end up minimizing some continuous surrogate loss or surrogate objective instead. The question that arises then is: How does the solution to the surrogate problem relate to the solution to the original problem we actually care about? Our research group has developed several fundamental principles and a general framework for constructing good surrogate loss functions that lead to both computationally efficient and statistically consistent learning algorithms.
In particular, our insights and contributions include among others the following: (a) defining the notion of convex calibration dimension of a loss matrix that impacts both the computational and statistical hardness of learning for that loss; (b) the design of convex calibrated surrogate losses for a variety of machine learning problems such as multiclass learning with a reject option and hierarchical classification; (c) a general recipe for constructing r-dimensional convex calibrated surrogate losses for any target loss matrix of rank r, leading to computationally efficient and statistically consistent learning algorithms for a variety of challenging learning problems including subset ranking and multi-label learning (see figure below); (d) establishing deep connections between surrogate loss functions in machine learning and proper scoring rules in the field of property elicitation; and (e) clarifying the role of the scoring function class when using surrogate losses in the context of H-consistency (as opposed to Bayes-consistency, which is what calibrated surrogate losses are generally designed to achieve).
Three of our papers in this research area have been selected for spotlight presentations at the Neural Information Processing Systems (NeurIPS) conference.
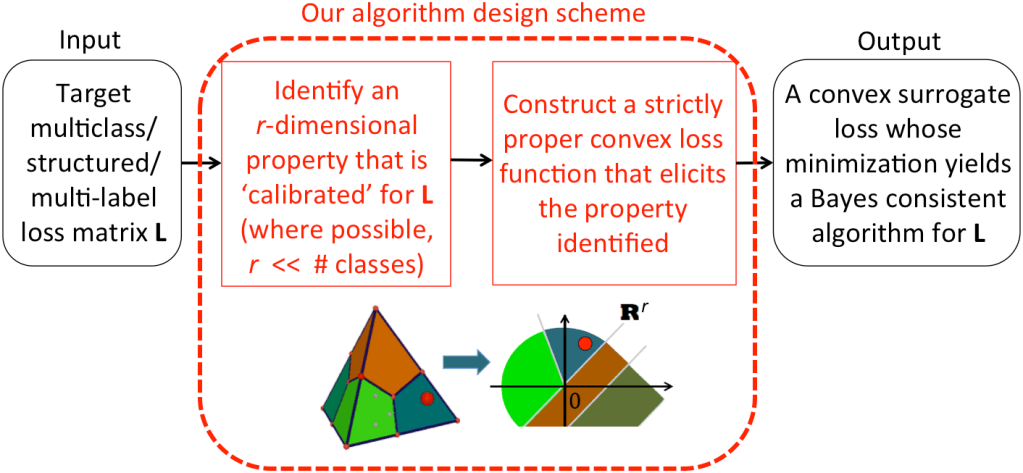
Our general scheme for designing computationally efficient and statistically consistent learning algorithms for multiclass/structured prediction/multi-label learning problems with a general target loss matrix L.
Relevant Publications
- Harish G. Ramaswamy, Mingyuan Zhang, Shivani Agarwal, and Robert C. Williamson.
Convex calibrated output coding surrogates for low-rank loss matrices, with applications to multi-label learning.
In preparation. - Shivani Agarwal.
Efficient PAC learning for realizable-statistic models via convex surrogates.
In Advances in Neural Information Processing Systems (NeurIPS), 2025.
[pdf] - Mingyuan Zhang and Shivani Agarwal.
Bayes consistency vs. H-consistency: The interplay between surrogate loss functions and the scoring function class.
In Advances in Neural Information Processing Systems (NeurIPS), 2020.
Spotlight paper.
[pdf] - Mingyuan Zhang, Harish G. Ramaswamy, and Shivani Agarwal.
Convex calibrated surrogates for the multi-label F-measure.
In Proceedings of the 37th International Conference on Machine Learning (ICML), 2020.
[pdf] - Harish G. Ramaswamy, Ambuj Tewari, and Shivani Agarwal.
Consistent algorithms for multiclass classification with an abstain option.
Electronic Journal of Statistics, 12(1):530-554, 2018.
[pdf] - Harish G. Ramaswamy and Shivani Agarwal.
Convex calibration dimension for multiclass loss matrices.
Journal of Machine Learning Research, 17(14):1-45, 2016.
[pdf] - Arpit Agarwal and Shivani Agarwal.
On consistent surrogate risk minimization and property elicitation.
In Proceedings of the 28th Annual Conference on Learning Theory (COLT), 2015.
[pdf] - Harish G. Ramaswamy, Ambuj Tewari and Shivani Agarwal.
Convex calibrated surrogates for hierarchical classification.
In Proceedings of the 32nd International Conference on Machine Learning (ICML), 2015.
[pdf] - Harish G. Ramaswamy, Balaji S. Babu, Shivani Agarwal and Robert C. Williamson.
On the consistency of output code based learning algorithms for multiclass learning problems.
In Proceedings of the 27th Annual Conference on Learning Theory (COLT), 2014.
[pdf] - Harish G. Ramaswamy, Shivani Agarwal and Ambuj Tewari.
Convex calibrated surrogates for low-rank loss matrices with applications to subset ranking losses.
In Advances in Neural Information Processing Systems (NIPS), 2013.
Spotlight paper.
[pdf] [spotlight slides] - Harish G. Ramaswamy and Shivani Agarwal.
Classification calibration dimension for general multiclass losses.
In Advances in Neural Information Processing Systems (NIPS), 2012.
Spotlight paper.
[pdf] [spotlight slides]